Write a program in C to create two sets and perform the Union operation on sets.

 Logic

The union of two sets X and Y is equal to the set of elements that are present in set X, in set Y, or in both the sets X and Y. This operation can be represented as;

X ∪ Y = {a: a ∈ X or a ∈ Y}

Let us consider an example, say;  set A = {1, 3, 5} and set B = {1, 2, 4} then;

A ∪ B = {1, 2, 3, 4, 5}

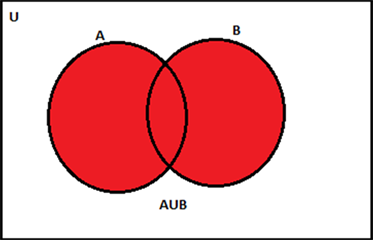
Now, let us learn how can we represent the union of two sets in a Venn diagram.

Program

#include<stdio.h>

#include<conio.h>

void main()

{

   int a[10],b[10],i,c[10],j,k=0,n1,n2;

    

        // taking input set A

    printf("Enter number of  element of set A\n");

   scanf("%d",&n1);

   printf("Enter the element of set A \n");

   for(i=0;i<n1;i++)

      scanf("%d",&a[i]);

 

        // taking input set B

    printf("Enter number of element of set B\n");

   scanf("%d",&n2);

   printf("Enter the element of set B \n");

   for(i=0;i<n2;i++)

     scanf("%d",&b[i]);

 

   // logic for calculate union

    // copy the element of set A in set C

   for(i=0;i<n1;i++)

   {

       // repeted element is not allowed so we check is any value repeted

      for(j=0;j<k;j++)

      {

         if(c[j]==a[i])

            break;

       }

       if(j==k) //if not repesated then store value in set c

       {

          c[k]=a[i];

          k++;

       }

    }

    // copy element of set B in set C

   for(i=0;i<n2;i++)

   {

       // check for repeted element

      for(j=0;j<k;j++)

      {

         if(c[j]==b[i])

           break;

      }

     if(j==k) // if element is not repeted then store in set C

     {

       c[k]=b[i];

       k++;

     }

   }

 

   // printing of union of set A and set B

   printf("Union of set A and B is:-\n");

    for(i=0;i<k;i++)

      printf("%d ",c[i]);

}